Straight-line grammar

Straight-line grammars (SLG) are formal grammars that do not branch (every non-terminal has only one associated production rule) nor loop (if non-terminal A appears in a derivation of B, B does not appear in a derivation of A). Such grammars generate only one sequence, and this property makes them of interest in fields like Kolmogorov complexity, Lossless data compression, Structure discovery and Compressed data structure.

The problem of finding a SLG of minimal size is called the Smallest grammar problem.

Formal Definition

A Grammar G is a SLG iif:

1. for every non-terminal $N$ , there is at most one production rule that has $N$ as its left-hand side

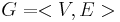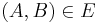2. take the graph $G=<V,E>$ , with $V$ the set of non-terminals and $(A,B) \in E$ if $B$ appears at the right-hand side of a production rule for $A$ . $G$ must be acyclic.

A SLG in Chomsky normal form is equivalent to a straight-line program. In general, the only type of grammar that are considered are context-free grammar.

A list of algorithms

Sequitur
Lempel-Ziv-Welch algorithm creates a context-free grammar in a such deterministic way that it is necessary to store only the start rule of the generated grammar.
Byte pair encoding